限界耐力計算法サポート会員
 限界耐力計算法
限界耐力計算法

 「仕様型設計」「性能型設計」
「仕様型設計」「性能型設計」 
「性能型設計」については、「性能規定型設計」「性能指向型設計」、あるいはたんに「性能設計」とも呼ばれています。一方、「仕様型設計」のほうについては、これを「性能設計」と対比させるために「仕様設計」ということもあるようです。

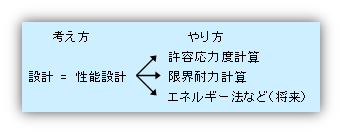
 (1) が性能設計の考え方の基本となる部分で、限界耐力計算法は (2) に含まれることになります。(3) が「社会的なシステム」となります。つまりこの三位一体によって始めて性能設計が機能するわけです。さらに、性能評価を「建築物の目標とする構造性能が実現されているか否かを評価する方法」と位置づけると、その一部に「性能検証」という作業があります。限界耐力計算法はこの「性能検証」に該当します。
(1) が性能設計の考え方の基本となる部分で、限界耐力計算法は (2) に含まれることになります。(3) が「社会的なシステム」となります。つまりこの三位一体によって始めて性能設計が機能するわけです。さらに、性能評価を「建築物の目標とする構造性能が実現されているか否かを評価する方法」と位置づけると、その一部に「性能検証」という作業があります。限界耐力計算法はこの「性能検証」に該当します。
 許容応力度計算法とは「仮定した荷重による応力度が許容応力度内にあることを検証する」という考え方ですが、これは「応答値が限界値を下回ることを検証する」という性能設計の考え方に合致しています。つまり許容応力度計算法とはいえ、明らかに、それによって得られる何らかの「性能」を期待していることになるのですが、しかしこれを「性能設計」とは呼ばないことになっています。その成果にたいして「性能」という明示的な表現が与えられていないから、というのがその理由であると考えられるからです。
許容応力度計算法とは「仮定した荷重による応力度が許容応力度内にあることを検証する」という考え方ですが、これは「応答値が限界値を下回ることを検証する」という性能設計の考え方に合致しています。つまり許容応力度計算法とはいえ、明らかに、それによって得られる何らかの「性能」を期待していることになるのですが、しかしこれを「性能設計」とは呼ばないことになっています。その成果にたいして「性能」という明示的な表現が与えられていないから、というのがその理由であると考えられるからです。
そこで、これからはそれを「性能」という観点から表現・評価することにしよう、というのが今いわれている「性能設計」の基本精神なのです。けっして、「許容応力度計算か限界耐力計算か」という選択が性能設計の分岐点になるわけではありません。
べつの言い方をすれば、性能設計の精神とは、「まずやり方を変えよう」というところにあるのではなく、「まずものの見方を変えよう」というところにあるのです。ものの見方を変えれば、おのずとやり方も変わってくるかもしれません。そしてその際に大切なのは、やり方に選択の幅があることです。
最近では、中・低層はもとより高層建物においてもいろいろなやり方で解析を容易に行えるようになりました。これもパソコンの性能が著しく向上し、ソフトウェアも低価格になり、限界耐力法に代表される高度な(と誤解されているだけかもしれませんが)解析を行うだけの環境を整えることは、誰もが容易にできるようになりつつあります。
![]()
限界耐力計算

1.長期・積雪時・暴風時については、今までどおり許容応力度計算をしなさい。
2.積雪時・暴風時については、今までどおりの許容応力度計算を行なうほかに、さらに高レベルの荷重レ
 ベルを想定し、それによる応力が部材の終局耐力を超えないことを確認する。
ベルを想定し、それによる応力が部材の終局耐力を超えないことを確認する。
3.今までの許容応力度計算法における「地震力にかんする一次設計」に代わるもの。地震力とそれに
 よる各階の層せん断力を あたらしい方法 によってもとめ、その時の応力度が短期の許容応力度内に
よる各階の層せん断力を あたらしい方法 によってもとめ、その時の応力度が短期の許容応力度内に
 あることを確認する。さらに、その時の層間変形角が1/200以内であることを確認する。
あることを確認する。さらに、その時の層間変形角が1/200以内であることを確認する。
4.地下階の地震力にたいしては今までどおり許容応力度計算をしなさい。
5.今までの許容応力度計算法における「保有水平耐力の検討」に代わるもの。地震力とそれによる各
 階の層せん断力を あたらしい方法 によってもとめ、その時の層せん断力が保有水平耐力内にあるこ
階の層せん断力を あたらしい方法 によってもとめ、その時の層せん断力が保有水平耐力内にあるこ
 とを確認する。
とを確認する。
6.建設省告示 平12第1459号「建築物の使用上の支障が起こらないことを確かめる必要がある場合
 及びその確認方法を定める件」に部材のたわみ量の制限がうたわれているが、これは、許容応力度計
及びその確認方法を定める件」に部材のたわみ量の制限がうたわれているが、これは、許容応力度計
 算法の場合と同じ。
算法の場合と同じ。
7.風や地震にたいする外装材などの安全性については、基本的には許容応力度計算法の場合に同じ。

 建物に作用する地震の大きさ(入力値)をもとめる あたらしい方法
建物に作用する地震の大きさ(入力値)をもとめる あたらしい方法

 その地震にたいする建物の応答値をもとめる あたらしい方法
その地震にたいする建物の応答値をもとめる あたらしい方法
が旧来の許容応力度設計法から変わったところとなります。また、積雪荷重と風荷重の規定は、

この表で見るとおり、『きわめてまれに発生する』荷重の大きさは、『まれに発生する』荷重を 1.4 倍(積雪)もしくは 1.6 倍(風)したものとなっています。その根拠は、積雪にかんしては、
 50 年再現期待値と 500 年再現期待値の比率は、多雪地域において 1.35、その他の地域において 1.44 であるため、規定の明確さと推定値の精度を考慮して、最大級の垂直積雪量は中程度の垂直積雪量の 1.4 倍とした。
50 年再現期待値と 500 年再現期待値の比率は、多雪地域において 1.35、その他の地域において 1.44 であるため、規定の明確さと推定値の精度を考慮して、最大級の垂直積雪量は中程度の垂直積雪量の 1.4 倍とした。
となっています。ここで、『きわめてまれに発生する』荷重が500 年再現期待値と定義されていることから、『きわめてまれに発生する』荷重とは建設予定地で将来想定されるであろう最大の荷重であることが理解できます。さらに、長期荷重・積雪荷重・風荷重にかんしては、許容応力度計算と限界耐力計算の違いはほとんど何もない、許容応力度計算そのものです。一方、地震に関する計算は新しくなっています。この新しくなった内容は次の図のように2点にまとめることができます。
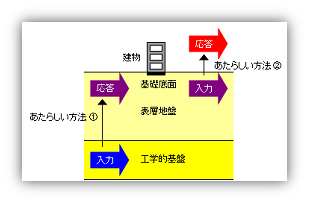
図で見るとおり、地表面での地震の大きさ(建物にたいする入力値)も、じつは工学的基盤 注) で入力された地震にたいする表層地盤の『応答値』なわけだから、『あたらしい方法』とは、いずれも『応答値をもとめる方法』であり、応答値をもとめるとは、『工学的基盤に入力された地震動が、表層地盤においてどれくらい増幅され、さらに建物に伝わった時にどれくらい増幅されるか』となります。
工学的基盤と表層地盤については、地震波は、地下のどこか深いところから地盤を伝わって地表面に到達するものと考えられます。この『地下のどこか深いところ』を『工学的基盤』、そこから地表面までを『表層地盤』と呼ぶことになっています。
そして工学的基盤とは、たとえば岩盤のような『かたい地盤』になるようだけど、『工学的』という名前のとおり、『工学モデル上それより先は考えなくてもよいと思われる程度にかたい地盤』」のことです。(杭基礎における杭の支持地盤程度の地盤)
ちょっと注意が必要なのは、限界耐力計算法では、地震の加速度によって地震動の大きさをあらわすことになっています。加速度は、「ガル(cm/sec2)」という単位 であらわしますが、これまでの構造計算では、「地震の加速度」というものを直接取り扱うことはなかったのです。地震力の大きさは『標準層せん断力係数(地上部の最下階に作用する層せん断力の建物重量にたいする比)』という形であらわされていました。
注)「ガル」は、いわゆるSI単位ではありませんが、例外として使用が認められています。公式なSI単位系では、加速度の単位は「m/sec2」になります。
すなわち、これまでの構造計算では、『一次設計に使用する地震力は、標準層せん断力係数を 0.2 を基本としてさだめる』となっていました。この地震の大きさとはどれくらいのものなのかというと、地表面での加速度がだいたい 80 から 100 ガル程度で、それが建物に入力された時に、最下階でだいたい 2.5 倍くらいに増幅された状態を考えています。
この地震の規模を震度階であらわすと、だいたい震度 5 の弱に対応します。
現在では、気象庁の震度階も地動加速度と関連づけてきめ細かく決められています。そんな時代に、『これじゃいくらなんでもだいたいが多すぎやしないか』というので、『これからはちゃんと加速度で表現しよう』となったわけです。
応答スペクトル

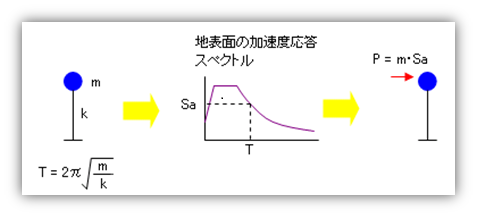
振動解析の理論によれば、一質点系(平屋の建物)の弾性応答値は建物の「固有周期」をパラメータにしてあらわすことができます。
そこで、下の図にあるようなモデルを考えます。これは、固有周期が短い順に左側から一質点モデルを並べ(バネの長さが短いものはバネ定数が大きくなり固有周期が短くなる)、これらに同じ地震波を作用させてその応答の最大値を調べようとするものです。
この方法で、『地表面の加速度応答スペクトル』を定義します。建物の固有周期は、質量 m とバネ定数 k からもとめることができます。これを加速度応答スペクトル上にプロットすれば、対応する加速度応答 Sa を求めることができます。
加速度に質量をかけたものが『力』なのだから、地震による外力 P はつぎのとおりで、これがそのまま『地震時の層せん断力』になります。
ここまでの手法は、一質点系、つまり平屋の建物について成り立ちます。 多質点系、つまり二階建て以上の建物ではこうはいきません。そこで、多質点系の建物の場合には、『平屋の建物に変換』となります。(下図参照)。つまり、多質点系を等価な一質点系に置き換えます。
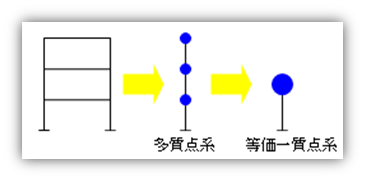
ではどのようにして一質点系に置き換えるのか、ということになりますが、限界耐力計算では『モード合成法』を利用します。
『モード合成法』

『モード合成法』とは、質点系モデルの『質点』とは、建物の床位置にその階の質量を集中させたものなのだから、質点の数は建物の階数にひとしくなります。この質点は水平方向にのみ移動するものと仮定しているのですが、これを『一つの質点は(水平方向という)一つの自由度だけもっている』といいます。ですから、三質点系のモデルならば、それは合計三つの(水平方向にかんする)自由度をもっていることになります。ところで、このような質点系モデルは、その自由度の数(つまり質点の数)にひとしいだけの『固有周期』と『固有モード』をもっています。(これは「固有値解析」という数学的な手法によって得ることができます)
『固有モード』は別名『固有振動形』とも呼ばれるように、各次の固有周期における質点の相対的な変位量 注) をあらわしたものと考えることができますが、下の図に見るように、これには以下のような特徴があります。
1.一次の固有モードは一方向に押された単純な形をしている。
2.次数が大きくなるにつれてその形が複雑になります。
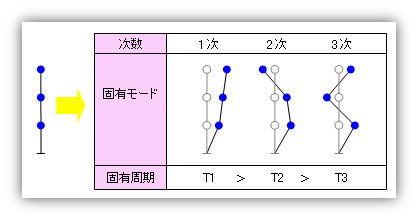
注)絶対的な変位量ではなく、各質点の変位量の比、つまり「全体としてこんな形になる」ことをあらわしている無次元量、ということです。私たちがよく使う「Ai分布」のような性格の値です。なお、上の図では片方向しか描いていませんが、もちろん、中心線にかんして左右対称に振動するのです。
例えば、釣竿を手に持って垂直に立て、手を動かしてそれを揺らした状態を考えてみると、下図にあるように、釣竿が短い場合は手の動きと同じ方向に「すなおな揺れ方」をします。しかし釣竿が長くなると、根元に近い部分はそのまま手の動きについてきますが、先端の方は遅れてついてくるため、手の動かし方によっては全体として「ヘンな揺れ方」をすることがあります。
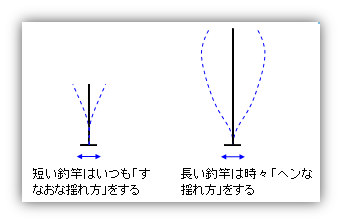
この『すなおな揺れ方』が『一次モード』です。そして、釣竿が長くなるにつれてなぜ『ヘンな揺れ方』が出てくるのか、それはそこに『高次(二次以降の)のモードが混ざってくる』からでした。釣竿の長短とはもちろん固有周期の長短をあらわして、『短い釣竿』とは『固有周期が短い低層の建物』、『長い釣竿』とは『固有周期が長い高層の建物』のたとえとなります。ここから、『固有周期が長い高層の建物には高次のモードの影響があらわれてくる』ということですが、これをもう少し一般化すれば以下のようなこととなります。 各次の固有モードとは質点系の『行動パターン』のようなもので、質点系の『ふるまい(振動)』は、必ずこれらの『行動パターン』の組み合わせであらわせることができます。つまり、各次のモードの影響度をあらわすなんらかの係数をもとめ、それを固有モードにかけて全次数分足し合わせれば、それが質点系の振動になるのです。これが『モード合成法』別名『モーダル解析』で、具体的な計算としてはつぎのような図になります
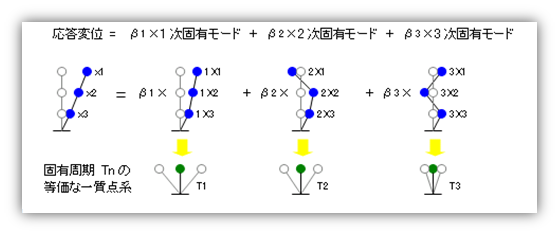
上の図にある「β1・β2・β3」が先に述べた『各次の固有モードの影響度をあらわす係数』(刺激係数)ですが、上図の下段にあるような、『各次の固有周期をもった等価な一質点系の応答値』でした。そしてこの『等価な一質点系』とは、下図にあるような、『等価な質量と剛性をもち、その次数に固有の振動形を保ったまま振動している質点系』になります。
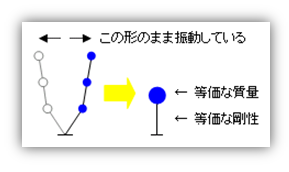
これは『一質点系の応答値』なのですから、例の『応答スペクトル』によってもとめることができます。
質点系の応答値

質点系の応答値は、
 1.固有周期
1.固有周期
 2.固有モード(振動形)
2.固有モード(振動形)
 3.応答スペクトル
3.応答スペクトル
の三点セットがあればもとめられる、ということになります。また、次数が大きくなればなるほど、そのモードが応答値に与える影響は少なくなるという性質があります(だから「建物の一次固有周期」のことをたんに「建物の固有周期」と呼んでいるのです。)
固有周期の短い低層の建物にだって、(平屋でない限り) 二次や三次の固有モードはありますが、それらの影響度は一次のモードに比べて相対的に少なく、結果的に無視できる程度のものとなります。場合によっては、各次数の足し合わせというような面倒なことを行わず、一次モードだけ考えればいいことになります。これに対し、固有周期の大きい高層の建物の場合は、一次モードだけ考えていたのでは「建物本来の揺れ方」を把握できません。そのため、二次とか三次まで考慮する必要があります。
固有周期の長い高層の建物では二次や三次のモードも無視できなくなるということから、限界耐力計算法は、『二次や三次のモードが無視できなくなるような高層の建物には適用できない』ということになりますが、これが、限界耐力計算法の適用を高さ60mまでの建物に限定し、それを超える高層建築物については振動解析を行うこと、としている現行規定の根拠となっています。
弾性(損傷限界)における応答値の求め方
(1)一次モードだけを考えている。
(2)その場合の振動形は、固有モードではなく、想定した外力分布のもとでえられる建物の実際の変位量から定めている。
ここにはもちろん、『この仮定にもとづいた結果が、実際の振動解析からえられるものとよい近似をしめす』という裏づけがありますが、大事なのは、『一次モードだけを考えている』ということです。
(ただし、二次以降のモードをまるきり無視しているのかというと、そういうわけでもないのです。その理由は、上の (2)にある「想定した外力分布」というところに隠されています。)
具体的に応答値をもとめる手続きを追ってみると、
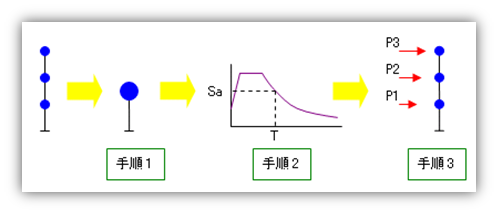
となります。もとめているのは、手順 3 にある『各質点、つまり各階の床位置に作用する地震外力の値』です。
ここで、地震外力とは各階の質量に地震の加速度をかけたものとなり、『各質点に作用する応答加速度の値』とも考えられます。応答加速度の値は加速度応答スペクトル図からもとめる(手順 2)しかありません。しかし応答スペクトルは一質点系を対象にしたものですから、まず建物を一質点系に置き換える(手順 1)必要があります。
整理すると

 手順 1 建物を一質点系に置き換えて固有周期をもとめる。
手順 1 建物を一質点系に置き換えて固有周期をもとめる。

 手順 2 その固有周期に対応する加速度応答を応答スペクトルからもとめる。
手順 2 その固有周期に対応する加速度応答を応答スペクトルからもとめる。

 手順 3 一質点系の加速度応答を多質点系の加速度応答にもどし、外力をもとめる。
手順 3 一質点系の加速度応答を多質点系の加速度応答にもどし、外力をもとめる。
となります。それでは、各手順を具体的に見ていきます。
 外力分布を決める
外力分布を決める 
限界耐力計算法では、『振動形(地震時の水平変位の分布形)を、想定した外力分布のもとでえられる建物の実際の変位量からさだめる』のです。この『想定した外力分布』とは、『Ai 分布』です。ただし、限界耐力計算法ではこれを Ai といわずに bdi といっています。名前が違うだけでなく中身も多少違うようです。
その違いは、Ai は『層せん断力の分布』をあらわしているが、bdi は『加速度の分布』をあらわしているということとなっていますから、外力分布として Ai を使っても bdi を使っても、結果(各階の層せん断力)は同じになります。
解説 平12建告第1457号第2の表中に規定される加速度の分布 bdi は、昭55建告第1793号第3に規定される層のせん断力分布係数分布を表す係数を層の水平力分布を表す係数に変換したものです。従って、従来の Ai 分布を求める計算方法に従って求めた各層のせん断力分布と、平12建告第1457号第2の表中に規定される加速度の分布 bdi により求めた各階の水平力の和として求めた各階のせん断力の分布は等しくなります。
ここで例として、地上三階・高さ12mの建物で各階の建物重量が全部等しいとした場合の bdi の値は下の図のようになります。
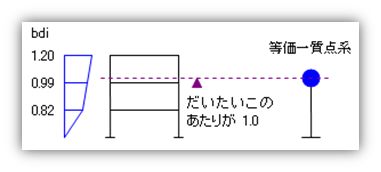
『Ai を使っても bdi を使っても結果は同じ』ですが、上の計算結果を見ると、少なくとも見かけ上の両者の値は違っています。『Ai は必ず最下階で 1.0 になるが、 bdi は建物の途中で1.0 になる』からです。これは、Ai の値は一階の層せん断力係数が基準になるので一階を 1 にするが、bdi の値は建物の代表点(つまり等価一質点系の質点位置)が基準になるので建物の途中を 1 とし、私たちは、最終的には各階に作用する加速度の値を決めますが、最初にいきなり bdi、つまり『各階の加速度の分布係数』を計算しています。すなわち、『各階の加速度の絶対的な値は分からないが、各階の値の相対的な比なら分かっている・あるいは分かったことにしている』わけです。さらに、この値は、モード合成法によりもとめられる実際の加速度の分布とよく一致しやすいことがわかっています。なぜなら、Ai分布がどのようにして導かれたかと言うと、建物実際の地震波形を入力する。その時、建物に生じる最大地震力が解かります。これを、いろいろな地震波形を入力して同様に調べ、建物も数階~10階ぐらいの建物をいろいろ想定し、それらを同様に調査します。想定し調査したものを統計的に処理し、導かれたのがAi分布であるからです。
bdiは、Aiを『各階の加速度の分布係数』にして表現しただけで、一致するのも当然といえます。またこの分布には、一次だけでなく二次以降のモードも含まれています。限界耐力計算法は、『二次以降のモードは無視している』といいながらも、実際にはこの bdi によって二次以降の影響も間接的に考慮していることになります。
■ bdi の値を何倍にすれば本当の加速度応答になるか、それを知ることが必要です。■
 手順2
手順2 
(2) その外力分布を作用させて変位量をもとめる
これは、bdi が各階の加速度の加速度の分布を直接あらわしているのですから、それに各階の質量をかければ、それがそのまま『外力分布』になります。これを作用させて各階の変位量をもとめます。(固有振動形にとって必要なのは変位量の値そのものではなく『各階の変位量の比』です。さらに、いまは弾性範囲(損傷限界まで)を対象にしていますから、外力と変位は比例します。結局、この外力の値を何倍あるいは何分の一にして計算しても結果は同となります。
 手順3
手順3 
(3) 等価一質点系の質量と剛性をもとめる
えられた各階床位置の基礎面からの相対変位量 δdi (最後の添え字 i はそれぞれの階の値であることをあらわします)と各階床位置に集中させた質量 mi から、等価一質点系の質量をもとめることができます。これを「有効質量( Mud )」と呼んでいます。この値は、平屋の建物では一階の質量( m1 )にひとしく、二階建て以上のならば各階の質量の総和(Σmi )よりも必ず小さくなります。 また、等価一質点系のパネ定数は以下のようにしてもとめます。『各階の外力により水平方向に変位している多質点系モデル』は、『その外力の総和(一階の層せん断力にひとしい)によって水平方向になんらかの変位を生じている一質点系』に同じとなります。
これは『代表点の変位』ですから、『代表変位(⊿d )』と呼んでいます。
結局、『層せん断力を代表変位で割ったものが等価一質点系のバネ定数である』ということになりますが、これを図示してみると
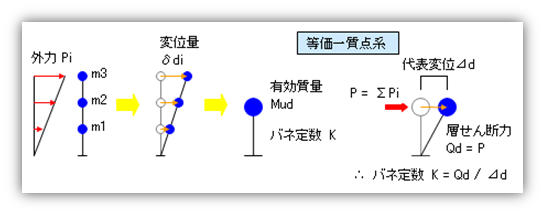
となります。
 手順4
手順4 
(4) 等価一質点系の固有周期をもとめる
質量とバネ定数がわかれば、等価一質点系の固有周期 Td は以下のように簡単にもとめることができます。
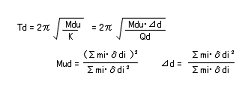
 手順5
手順5 
(5) 応答スペクトルから等価一質点系の応答加速度をもとめる
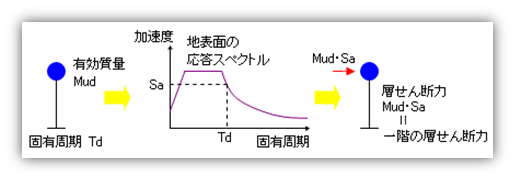
解説地表面での応答スペクトルとは、工学的基盤の応答スペクトルに増幅率 Gs をかけたものです。上でもとめた固有周期 Td を横軸にプロットし、地表面での応答スペクトルとの交点から加速度応答スペクトル Sa をもとめます。これで、「等価一質点系に作用している加速度 Sa」が分かりました。「加速度に質量をかけたものが力」ですから、いま作用している力は「Mud・Sa」です。一質点系ですから、これは生じている層せん断力の値にひとしくなります。この等価一質点系に生じている層せん断力の値とは何かというと、本当の建物に作用している力の総和、つまり「本当の建物の一階の層せん断力」と同じ(等価)です。
 手順6
手順6 
(6) 各階の応答加速度と外力・層せん断力をもとめる
解説 bdi とは「各階の加速度の分布を直接あらわした値」なのですから、あとは簡単です。
Sa にその階の bdi をかけたものがその階の応答加速度になる
応答加速度にその階の質量 mi をかけたものが外力になる
外力を上の階から足し合わせたものが層せん断力になる
となりますが 、
上のようにして得られた「一階の層せん断力」は、前ステップでもとめた「等価一質点系の層せん断力」の値とは合いません。なぜなら、等価一質点系では「有効質量( Mud )」を使って計算しているのに、ここでは「本当の総質量(Σmi )」を使ったことになるからです。そこで、一質点系から多質点系にもどすにあたり、有効質量と総質量の比、つまり Mud/Σmi をかけてやることにします。この値を「有効質量比」といいますが、これは平屋の建物で 1.0 になり、高層になるにつれて小さくなります。限界耐力計算法では、bdi にこの有効質量比をかけたものを Bdi といっており、下のように定義されます。
Bdi = ( Mud/Σmi )・bdi
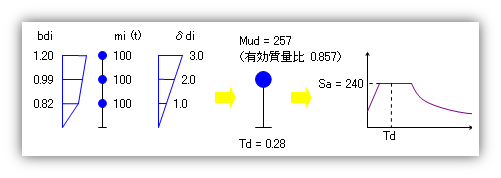
三階建ての建物を例に計算すると、bdi にもとづく外力を作用させた時の各階床位置の変位量 δdi が、仮に下から「1:2:3」になっていたとすると、Mud は下のようになり、この時の固有周期は(変位と外力の単位を適当に仮定すると)0.28 秒になります。これを、略算による増幅率をもちいた「まれに起きる地震」の応答スペクトル上にプロットすると、(応答スペクトル図の最大加速度は 160×1.5 = 240gal で、Td < 0.64 ですから)応答加速度は240gal、つまり 2.4 m/sec2 です。
これにもとづいて各階の Bdi と加速度・外力・層せん断力を計算すると下のようになります。
| 階 | Bdi | 加速度 (m/sec2)= Sa・Bdi | 外力 (kN)= mi・Sa・Bdi | 層せん断力 (kN) | 層せん断力係数 |
| 3 | 1.028 | 2.47 | 247 | 247 | 0.252 |
| 2 | 0.848 | 2.04 | 204 | 451 | 0.230 |
| 1 | 0.703 | 1.69 | 169 | 620 | 0.211 |
解説 この表で、1 階の層せん断力の値と「Mud かける Sa」の値が少し違っていますが、これは、端数処理による誤差です。本当はちゃんと合うのです。念のため。ところで、このようにしてえられる設計地震力とはだいたいどの程度のものというと、上の表の右列にある層せん断力係数の値をみても分かるとおり、今までの許容応力度計算とだいたい同じ値 になります。これはいうまでもなく、「最初からそうなるように作られている」ためです。
捕捉すると限界耐力法では、前例の有効質量比のほかにも、一質点系から多質点系にもどす際に使われる係数があります。これには『p』『q』という素っ気ない名前が付けられていますが、これを使うと、さきほどの Bdi の式は以下のようになります。
Bdi = p・q・( Mud/Σmi )・bdi
先ほど、『限界耐力計算法による地震力は許容応力度計算法によるものとだいたい同じ値になるように設定されている』ということでしたが、低層の建物(つまり有効質量比の大きいもの)では許容応力度計算法によるものよりも大きくなってしまう傾向にあります。そこで、低層の建物でも許容応力度計算法と同じような地震力になるように、限界耐力計算法にもとづく地震力を低減しているのが係数 p なのです。
解説 この値は 5 階建て以上の建物で 1.0 、4 階建て以下の建物では 1.0 よりも小さな値になります。(さきほどの計算例では p の値が 0.90 ですので、これを適用すると一階の層せん断力係数は 0.19 になります。)許容応力度計算法よりも値が大きくなったところで、「それのどこが問題なのか」とおもいますが、「計算例と解説」によれば、「許容応力度等計算によってもこれまで特に構造安全上の支障はなかったことも考慮し、許容応力度等計算と同等の設計用地震力が得られるように、・・・」ということのようです(P.68)。これは、許容応力度計算法にたいする「気配り係数」というようなものです。
逆に、係数 q のほうは、有効質量比が小さくなる高層の建物にたいする補正係数なのです。先に話したように、高層の建物では二次以降のモードの影響が大きくなるため、限界耐力計算法をそのまま適用すると誤差が大きくなり、場合によっては地震力を過小に評価するおそれが出てきます。そこで、『実際の有効質量比が 0.75 未満の場合はそれを 0.75 として計算しなさい』ということにしたのがこの係数なになります。
具体的には、
有効質量比が 0.75 以上の場合は q を 1.0 とする
有効質量比が 0.75 未満の場合は q を 0.75・Σmi/Mud とする
となっています。
解説 これは有効質量比の逆数に 0.75 をかけただけですから、さきほどの Bdi の式をよく見ていただければ分かるとおり、結局は、「実際の有効質量比が 0.75 未満の場合はそれを 0.75 としなさい」という、それだけのことをいっているに過ぎません。 それから、ここまでふれませんでしたが、許容応力度計算法と同様な「地域係数 Z」というものもあります。これは、本来は応答スペクトルにたいして考慮すべきものですが、内容についてはすでにご存知のはずですから、説明は省略します。
弾塑性(安全限界)における応答値の求め方
ここまでで、弾性範囲(損傷限界まで)の求め方については終わりです。次は塑性範囲(安全限界)です。塑性範囲(安全限界)の応答の求め方も基本的には同じで、建物が塑性化するのは、その構成要素である個々の部材が塑性化するからです。ただし、『質点系モデル』」を対象としているわけですから、質点系モデルのバネ、つまり『各階のバネ定数の変化』という側面から塑性化をとらえることになり、『各階のバネ定数の変化』は、『層せん断力と層間変位の関係』としてあらわされます。
図は、 1 層 1 スパンの建物の頂部に地震力に相当する水平力を作用させ、その力を漸増させた時の層せん断力と層間変位の関係をあらわしたものです。
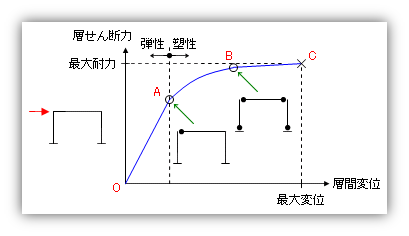
部材の応力がすべて弾性範囲内にあるのであれば、層せん断力と層間変位の関係は直線的に(線形に)変化します。この関係が『弾性』です。
しかし、外力の増加にともない、どこかの部材の応力が弾性限界を超えると、そこに『塑性ヒンジ』が作られます。これが上図の A 点です。この時点から層せん断力と層間変位の線形関係がくずれることになりますので、この点を『弾性限界(損傷限界)』と呼んでいます。
ここでさらに外力を増加させると、他の場所にも次々と塑性ヒンジが発生し、それが十分な数に達すると、『微小な外力の増加によって変形が大きく増大する』状態になります。つまり、層せん断力と層間変位のグラフがほとんど水平に近くなってきます。B 点がその始まりです。
しかし、この時点で建物が『こわれる(倒壊する)』のかというと、かならずしもそうではありません。『変形に追従できるとろまではついて行き、それができなくなった時にこわれる』ということになります。これが C 点です。
結局、この C 点が建物の『最大耐力』と『最大変位』をあらわしていることになります。また、この時の最大耐力を『保有水平耐力』と呼んでいます。」
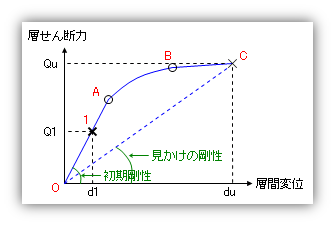
解説 限界耐力計算法の用語にもとづけば「安全限界耐力」「安全限界変位」ということになります。前回見てきたのは「弾性範囲」の出来事ですから、上のグラフでいえば、O-A 間にたいして適用される考え方です。上のグラフをもう一度下に描きなおしてみますが、これでいえば、バネ定数を Q1/d1、つまり「線 O-A の傾き」でとったことになります。これは「初期剛性」「弾性剛性」などと呼ばれます。
もっとも、鉄筋コンクリートの「ひび割れ発生後の剛性低下」を考慮した場合は「弾性剛性」と「初期剛性」は同じにならないのですが。
ここで、なんらかの方法で層せん断力と層間変位の関係を追跡し、上図にあるような最大耐力 Qu と最大変位 du の値がえられたとします。(もちろん、これは「普通の応力計算」ではもとまりませんが。とりあえず、「なんらかの方法でそれが分かったのだ」ということにしておきます。)
この点はもちろん「塑性域」にあります。そこで、これも弾性域と同じようにあつかうためにどうするのかというと、「原点と点 C をいきなり結んで」しまいます。つまり、「原点からいきなり C 点まで行ってしまった」と仮定するわけですが、この「線 O-C の傾き」、つまり Qu/du を「塑性時の剛性」ということにします。これは「本当の剛性」ではないので、「見かけの剛性」といえます。「見かけの剛性」という考え方で私たちに馴染みがあるのは、「耐震壁の剛性低下率」です。これは「ひび割れ発生後の剛性低下」を念頭に入れた「見かけの剛性/初期剛性」の値です。この「見かけの剛性」を「弾性剛性」に置き換えてしまえれば、あとは前回述べた「弾性応答」の考え方がそのまま適用できる、とするのが限界耐力計算法の基本的な考え方です。
ただしここで注意しておきたいのは、これを一次の固有モードとみなすためには、ここでも弾性応答の場合と同様な「各階の変位量の比例関係」が成り立っていなければならない、ということです。もう少し具体的にいうと、「各階がほぼ一様に塑性化する」ことが前提になっているのです。(厳密にはそうでもないけど)
上の図からも明らかなように、塑性時の剛性はかならず初期剛性よりも小さくなります。剛性が小さくなれば固有周期は長くなります。つまり、建物が塑性化すると「大きくゆっくり揺れるようになる」のです。
このように、限界耐力計算法では「弾塑性応答」も「弾性応答」とほぼ同様のあつかいができるように作られているのです。しかしこれだと、両者の区別がつかなくなって困る場合も出てきそうです。そこで、「使う記号を変える」ことになっています。
弾性時においては、「bdi」「Mud」「Td」などのように、「d」が含まれていました。
弾塑性応答では「d」の代わりに「s」を使うことになります。
「d」は「弾性( Dansei )」、「s」は「塑性( Sosei )」の略である、と覚えておくと便利です。たぶん、本当は「Damage」と「Safety」か何かの略なのですが、どう解釈しようと勝手ですから。
さらにここには、この「d」と「s」を除いた「総称」というものも存在しているために一層ややこしいのですが、ともあれ、一覧表を掲げると
| 弾性時 (d) | 塑性時 (s) | 総称 | 内容 | 「d」と「s」の比較 |
| bdi | bsi | bi | 外力分布 | 同じもの |
| Bdi | Bsi | Bi | 有効質量比×外力分布 | 有効質量比の値により変わる |
| δdi | δsi | δi | 各階の絶対変位 | δdi < δsi |
| ⊿d | ⊿s | ⊿ | 代表点の変位 | ⊿d < ⊿s |
| Mud | Mus | Mu | 有効質量 | どちらが大きいとはいえない |
| Td | Ts | T | 固有周期 | Td < Ts |
| p | p | p | 低層建物用の係数 | Tの値により変わる |
| q | q | q | 高層建物用の係数 | 有効質量比の値により変わる |
減衰とは、先ほどの釣竿の例にすると 釣竿を持った手を動かすとそれは揺れだしますが、しかしそのまま放っておけばやがて静止します。すなわち、『振動している物体は、外からあらたな力が加わらない限り、やがて静止する』のです。この現象を『減衰』と呼んでいます。これは、蹴り出したサッカーボールをそのままにしておけば、いつかはどこかで静止するはず、というのと原理的には同じですよね。この現象を物理学的にあらわせば、『振動エネルギーがさまざまな形(空気の摩擦・分子間の摩擦など)で熱エネルギーに変換され、失われるため(内部粘性減衰)』となりますが、振動工学上は、これを『振動を制止するような何らかの力がそこに作用しているためである』としています(減衰力と呼ぶ)。
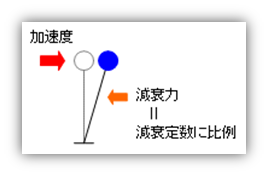
振動工学上では、この減衰力を「減衰定数」という指標値であらわしており、この値が 0 の場合は減衰がまったくない状態(つまり永遠に振動しつづける)、1 の場合は減衰力によってまったく振動が起きない状態をあらわす、と定義されていました。
結局、この値はかならず「0 より大きく 1 より小さい」ことになります。もちろん、減衰定数が大きくなれば応答値は小さくなります。それでは、実際に地震で揺れている建物の場合にこれがどれくらいの値をとるのかというと、2% から 5% の間くらい(つまり 0.02 から 0.05 くらい)とされています。(「くらい」とか「とされている」とかいうのは、そもそもこの値を厳密に把握することが困難だからです。) 減衰については、『振動特性係数』も限界耐力計算にもちいる『加速度応答スペクトル』も、みな『減衰定数を 0.05 (5%)』として作られているようですね。
しかし、弾塑性の応答値をもとめようとすると、減衰定数を一定にしたままではいけないみたいです。この『暗黙の減衰定数 0.05』のほかに、『弾塑性振動のエネルギー吸収による減衰機構』がでてくるようなのです。
「?・・・・・・????? 『弾塑性振動のエネルギー吸収による減衰機構』って?」
「その前に、『弾塑性振動とはそもそもどういうものなのか』を理解しないと無理なので簡単におさらいしましょう。」
限界耐力法では、弾塑性解析の手法として等価線形化法を採用しています。
この等価線形化法とは、
 等価線形化法
等価線形化法

層せん断力と層間変位の関係のもっとも単純な表現は、下図にあるように、弾性部分と塑性化後をあらわす二つの直線を使ったものとなる。(ただし地震力は正負方向に交替して作用するので、ここでは正負両側にこれをあらわすこととします。)
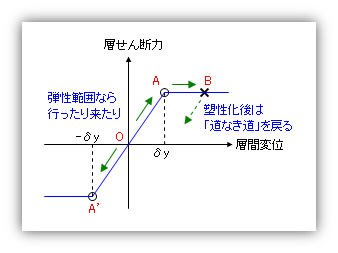
ここで、質点系に実際に地震波を作用させ、各時刻ごとの層せん断力と層間変位をここにプロットしたとする。 これが本当の『振動解析(弾塑性応答解析)』で、その応答結果をプロットしたものを『履歴ループ』と呼んでいるのだ。
もしこの時の応答値が弾性限の変位(上図の δy と -δy の間)内におさまっているのであれば、これは『ループ』にならず、たんに直線 A-A' 間を行ったり来たりする『直線』になります。これが『弾性応答』。
しかし、ある時点で地震の加速度が大きくなって弾性限を超え、上図の B 点に達したとする。そのまま同じ方向に加速度が作用しているのならこの直線上をどんどん進むだけなのだが、地震加速度は正負交替に作用するわけだから、どこかで『戻る』こととなる。これを『除荷』いいますが・・・・・。 この時に『もと来た道をそのまま戻る』のなら話は簡単。しかし、いったん塑性化してしまうと『もと来た道をそのまま戻る』わけではない。
ようするに、この先は『道なき道』を戻ることとなるのだが、かといって無茶苦茶に進むわけではなく、そこには『行動パターン』が存在する。これを種々の実験などによってさだめたものを『復元力特性』といい、各種のパターンにいろいろな名前(標準型・剛性劣化型・スリップ型など)がつけられています。
1つの例として『復元力特性』とは、次の図のようになる。
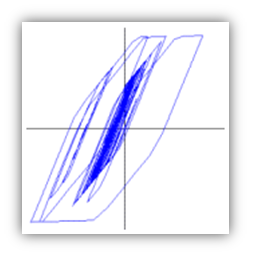
ともあれ、塑性域に入った後は、次の図左にあるような『なんらかのルール』にしたがって行動することとなりますが、それにもとづいた『行ったり来たり』を何度も繰り返していると、結果的には、次の図右の塗りつぶし部分のような、正負方向の最大変位点を頂点とする『閉じたループ』の中で行動しているように見えてくる。(先に掲げておいた実際の履歴ループと次の図を見比べてもらえば、このあたりはなんとなく納得していただけるはずです。)
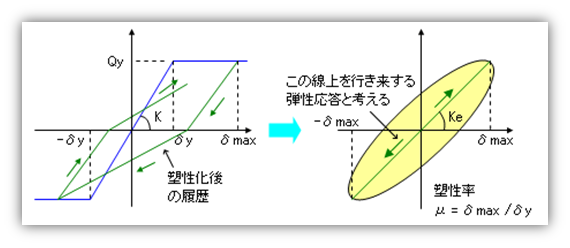
そこで、上図右にあるように、履歴ループの正負の最大変位点を結んだ原点をとおる直線を考えると、上図左にあるような塑性化後の履歴は、この直線上を行き来している弾性応答と実質的に同じと考えてもいいのではないか、となるわけです。これが『等価線形化法』と呼ばれる考え方。つまり、『弾塑性応答を等価な弾性応答(線形モデル)に置き換える』ということにほかならないのですが、これがそのまま、限界耐力計算で弾塑性応答をもとめるための基本アイディアになっています。
塑性化後の最大変位を弾性限の変位で割ったもの、つまり上の図でいえば δmax /δy になるが、これを「塑性率( μ )」といい、これを使って等価線形モデルの等価剛性( Ke )と等価固有周期( Te )をあらわすと、

注) μ はかならず 1 よりも大きくなりますから、先に述べた、「塑性域に入ると固有周期が長くなる」という事実は上の式からも裏付けられます。ところで、私たちは弾性剛性(初期剛性)の値ならすでに知っています。ですから、あとは「塑性率」が分かれば「等価剛性」がもとまることになりますが、ではどうしたら塑性率が分かるのかというと、これは「応答結果」ですから、振動解析をしない限り分かりません。しかしそもそも、私たちは振動解析を行なわずに応答結果をえようとしているのですから、これはまったく矛盾します。
そこで、なんらかの方法で等価剛性を「推定」しようとするわけですが、じつは、それが先に述べた「見かけの剛性」なのです。すなわち、「最大変位点と原点を結んだものの勾配」です。
つまり、限界耐力計算法では、最大変位点の剛性を「等価剛性」としているのです。結局、先にもとめた「見かけの剛性」は「塑性時の等価剛性」と同じで、それをもとにした固有周期は「塑性時の等価周期」である、ということになります。しかし、もしこれで話が全部終わるのだったら拍子抜けするくらいに簡単で、なにもあらためて「等価線形化法」などというものを持ち出すまでもなかったわけです。もちろん、話はこれだけでは終わりません。
たんに最大変位点と原点を結んで弾性応答にしただけでは、正しい弾塑性応答値をえることはできません。というのも、本当の弾塑性応答は「直線」ではなく「ループを描いている」からで、それを何らかの形で勘案しながら弾性に置き換えるのでなければ、とても「等価」とはいえません。 「ループを描く」とは、「それによってエネルギーの吸収が起きる」ということに他なりません。
 履歴減衰
履歴減衰

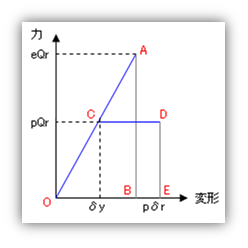
このグラフは、「建築物の構造関係技術基準解説書」(前掲書)にある「必要保有水平耐力」の説明図をそのまま写したものですが、この内容はおおむね以下のとおり。 作用地震力により、建物が原点 O から点 A まで変形したとする。この時に建物が受け取るエネルギーの総量は三角形 OAB の面積になる。これは『弾性変形』である。これにたいし、建物の塑性化を許容したとすると、原点位置から O-C-D のように進む。この時に建物が受け取るエネルギーの総量は四角形 OCDE の面積になる。ここで、建物に入力される地震のエネルギーが両者とも同じである、つまり三角形 OAB の面積と四角形 OCDE の面積が等しいとする。この時、弾性変形しか許容しないのであれば、この建物には eQr の耐力が必要とされることになるが、塑性変形を許容するのなら pQr の耐力でよいことになる。この pQr を『必要保有水平耐力』」といい、『pQr/eQr』を『構造特性係数( Ds )』という。 ところで、上の図はあくまでも『静的な力』、つまり『一方向にそのまま押して行った』場合のものなのだが、実際の地震力は正負交替に作用する。ではこの時にはどうなるのかというと、次のように考えればよい。
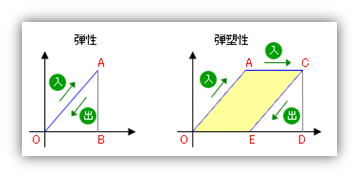
図の左が弾性の場合で、まず正方向に押されて原点から A 点に到達し、三角形 OAB のエネルギーを受け取ることとなる。ここで負方向に押されると再び同じ道をたどって戻るのだから、三角形 OAB のエネルギーを今度は『放出』する。これは収入と支出の帳尻が合って『プラマイゼロ』になっている状態といえる。
今度は図の右にある弾塑性状態を考えてみる。正方向に押された時に弾性限を超えてC点に到達したとする。この時に受け取るエネルギーは四角形 OACD となる。 ここで負方向に戻されたとすると、すでに述べたとおり、この時は『もとの道を戻らない』のだから・・・・・・ たとえば E 点まで戻ったとすると、この時に放出されるエネルギーは三角形CDEとなる。
ここでは、明らかに収入と支出の帳尻が合ってはいない。入ってきたものは四角形 OACD なのに、出て行ったものは三角形 CDE なのだから、この差し引き分、つまり上図の塗りつぶした範囲(四角形 OACE )に相当する面積分はどこかに『貯めこんでしまった』ことになるわけです。この、『貯めこんだ』というのはあくまで建物自身から見た表現ですが、これを建物の外側から見てみたらどうなるのか、というのが次の図となる。
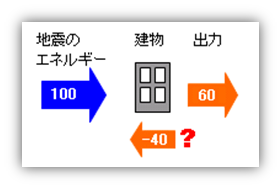
この様子を建物の外側から見ている人には、建物が『貯めこんだ』分は、たんに『消えてしまった』ようにしか見えない。しかし何もしないのにエネルギーが消えてしまうはないのだから、これは建物の内部にクッションのようなものがあって、それがエネルギーの一部を『吸収』した。と考えればよい。このクッションには建物の出力(つまり「応答」)を抑止するはたらきがあるのだから、機能的には『減衰』と同じ。いってみれば、これは『エネルギー吸収による減衰機構』となる。この機構は弾塑性応答の履歴ループによるものなので、先に述べたような通常の(空気の摩擦などによる)減衰と区別するために、とくに『履歴減衰』などと呼んだりしている。
等価線形化法の概念を再掲してみると
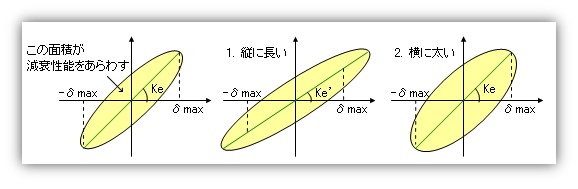
この様になる。さきほどの話からも推察できるとおり、このモデルのエネルギー吸収量は、ループで囲まれた面積分に相当する。この面積が大きいほど履歴減衰が大きく、応答が抑制される、ということです。
この面積が大きくなる条件は二つ。
1. 同じ形状なら、塑性率が大きい(つまり縦に伸びる)ほど大きくなる(上図中央)
2. 同じ塑性率なら、横幅が大きい(つまり太っている)ほど大きくなる(上図右)
『塑性化して変形量が大きくなると固有周期が伸びるので揺れが大きくなる』のといったばかりなのだが、上の 1 に見るように、ここでは逆に、『変形量が大きくなると減衰が大きくなるので揺れが小さくなる』ことになってしまう。 相反しているようですが、しかし、そういうこととなる。・・・・
結局等価線形化法とは、
弾塑性応答を、等価な剛性をもち、さらにその履歴ループの面積と等価な減衰性能をもった弾性応答に置き換えたものである と言える
 減衰による加速度の低減率
減衰による加速度の低減率

さて、これでようやく限界耐力計算法に戻れるのだ。限界耐力計算法では、加速度応答スペクトルに下式でもとめられる低減率 Fh をかけることになっている。
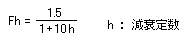
この式は減衰定数 h が 0.05 の時に Fh が 1.0 になるように作られている。前に、『限界耐力計算法の加速度応答スペクトルは減衰定数が 0.05 であることを前提に作られている』といったのはこれを指しています。だから、弾性応答の場合はとくにこの係数を意識する必要はなかったのだけど、弾塑性の場合には考えておく必要が出てきます。
さて、減衰定数の決め方には、『部材レベルで計算し、その重みづけの平均を建物の減衰定数とする』という方法と、『建物の減衰定数をいきなり決めてしまう』方法の二つがある。
しかし減衰定数という値のもつ精度を考えると、前者の方法はあまり現実的とは思えないので後者の方法について説明することにすると、減衰定数 h は下式でもとめることとなる。

注)告示本文では、上の式の「 γ 」が「 γ1 」、「 μ 」が「 Df 」と表記されていますが、「計算例と解説」の説明文では上のような表記になっています。こちらの方が馴染みがある記号なので、ここでは、こちらの表記を使いました。
この式の右辺第一項が『履歴減衰』、第二項が『通常の減衰』をあらわしている。塑性率は当然 1 以上の値をとるのだが、これが 1 であるという状態は『弾性』をあらわすこととなる。この時には履歴減衰の項が 0 になる、という仕組みになっているのが分かります。
前項で、『履歴減衰の大小は履歴ループの面積の大小によってあらわされる』ということ、そして履歴ループの面積の大小をあらわすには、『どれくらい縦に長いか』と『どれくらい横に太いか』という二つの尺度があることを説明しました。このうちの『どれくらい縦に長いか』をあらわしているのが上の式の 1-1/√μ という値で、この値は μ が大きくなるほど大きくなる。つまり、『どれくらい縦に長いか』塑性率が大きくなるとそれだけ履歴ループが縦に長くなり、面積が増えるので、減衰定数が大きくなる』ということをあらわしています。
では、この『塑性率』はどうやったら分かるのかというと、限界耐力計算法では、これを等価一質点系の代表変位と層せん断力の関係からもとめることになっています。
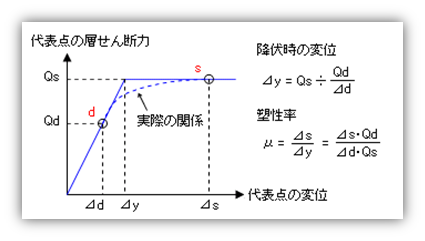
すでに建物の代表点の弾性時の変位をあらわす点 d と最大変位をあらわす点 s については知っている。そこで、まず原点と点 d を結び、これを『弾性時』をあらわす線とする。つぎに、点 s をとおる水平線を引く。これが最大耐力をあらわす線なので、これらの二つの線の交点から『降伏が始まる』とし、この時の変位を『降伏時の変位』とする。また、塑性率は最大変位をこの降伏時の変位で割ったものになりますが、これがだいたいどれくらいの値をとるのかというと、普通に設計されている建物なら 2 から 4 の間となる。
注) もちろん、層せん断力と変位の関係は実際にはこんな単純なものではなく、上図に破線で書き入れたようなものになるはずですから、これは層せん断力と変位の関係を「理想化」したものです。このようなモデルを「完全弾塑性」といいます。
つぎに、履歴ループが『どれくらい横に太いか』をあらわす係数「 γ 」のほうなのだが、これは『塑性化後にどのような戻り方をするか』によって決まります。限界耐力計算法では、この値は0.25 か 0.20 のいずれかの値をとることになっている。この値が大きいほど『履歴ループが横に太くなる、だから減衰が大きくなる、だから応答値が小さくなる』という仕組みになっているが、・・・・・・・・・
最後に、この使い分けにかんする告示の本文と「計算例と解説」の説明文(p.84)の両方をつぎの表でまとめてみることとしよう。」

解説 ここで上の説明に「ノーマルトリリニア型」という用語が出てきますが、これは「ノーマルなトリリニア型」という意味です。とりあえず「トリリニア」は後回しにして「ノーマル」の方を説明しますと、これは下にしめすように、「戻る時の剛性が初期剛性と同じになる」復元力特性のことです。それにたいし、戻る時の剛性が初期剛性よりも小さくなるものは「剛性劣化型」などと呼ばれます。
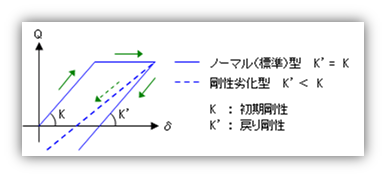
上の図からも分かるように、戻る時の剛性が初期剛性にくらべてあまり小さくならなければ、それだけ履歴ループが「横に太い」状態になって減衰が大きくなるわけで、そのあたりを根拠にして「 γ 」の値がさだめられていることになります。しかし上に引いた文章を読めば分かるとおり、このあたりは、「まあそんなような程度のもの」という値なのです。となると、私たちとしては、鉄骨造の純ラーメン構造なら 0.25 としても良いが、それ以外のケースでは、とくに明確な根拠にもとづかない限りは、安全側の処置として 0.20 をとっておく というようにしておけばいいのではないでしょうか。
![]()
 限界値
限界値

最大耐力
荷重増分解析におけるある荷重ステップにおいてどこかの階が最大耐力にたっしたなら、その時の状態が建物の最大耐力をあらわします。では、どのようにしたら『最大耐力にたっした』ことが分かるのかというと、それは『耐力が頭打ちになった』ことで分りました。
この、『耐力が頭打ちになる』ということは、下図にあるような層せん断力と層間変位のグラフ(Q-δ関係)が『横に寝てくる』 ということで、これをもう少し工学的な表現になおせば、『微小なせん断力の増加によって変位量が急激に増大する』こととなります。
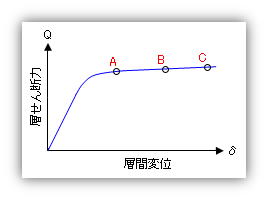
注) これが水平になると完全な「不安定構造」ですが、そのようになることはありません。あくまでも「水平に近くなる」だけです。その理由は先にもいいましたが、増分解析法では、各部材の塑性化後の剛性を完全に 0 にするのではなく、微小な剛性をもつものと仮定しているからです。
上図の A 点から「変位の急激な増大」が始まり、その後、さらに B・C 点を通過したとする。これを層せん断力(つまり「保有水平耐力」)の側から見るのであれば、 A・B・C 点のどこの値を採用しようとも、それはほとんど計算誤差の範囲内といえる。だから、従来の計算方法では、安全側として A 点の層せん断力を採用し、これを「保有水平耐力」としていた。
しかし限界耐力計算法では、保有水平耐力だけでなく、さらに「最大変位」の値も必要です。そこで、こんどは上のグラフを「変位」の側から見てみると、 A 点から C 点に向かう間は『微小なせん断力の増加によって変位が急激に増大する』のだから、 A・B・C 点の値はおおいに違ってきてしまう。そこで、『耐力と同じように、変形にだって限界というものがあるだろう』というふうに考えることとする。建物はそんなにどこまでも変形に追従できるわけではなく、ある限界にたっしたら壊れるはずだから、その限界を『最大変位』」と呼ぶこととなる。
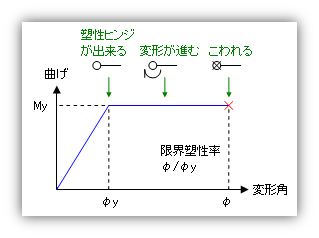
限界塑性率
部材端に塑性ヒンジが形成され、さらにその後外力が増加すると、下の図にあるように、その部分は一定の力を保ったまま変形(材端回転角)だけが増加する。しかしどこまでも変形に追従できるわけではなく、ある限度にたっすると破断するよね。部材の変形角と降伏時の変形角の比(下図でいえば φ / φy )が『塑性率』になるのだが、この用語を使えば、破断時の塑性率は『限界塑性率』ということになる。この値は部材の『塑性変形能力』をあらわすものといえる。つまり、限界塑性率が大きいほど、その部材は『塑性変形能力が高い=変形に追従できる=エネルギー吸収能力がある=靭性がある』、だから『好ましい』となる。
従来の計算方法では、この塑性変形能力を『構造特性係数(Ds)』という形で間接的に取り扱ってきました。(鉄骨の幅厚比などからもとまる)『部材ランク』と呼ばれる指標によって塑性変形能力をあらわし、その能力の高い部材が多いほど建物全体のエネルギー吸収能力も大きくなる。だからその分だけ、要求される保有水平耐力(つまり「必要保有水平耐力」、言い方を変えれば「層せん断力の応答値」)も小さくなるはずである、という考え方でした。
注) この「部材ランク」が具体的にどの程度の塑性変形能力をあらわしているのかというと、部材ランクが A のものの限界塑性率はだいたい 5 から 6 くらいになる、とされているようです。 これにたいし、「増分解析法」を使えば、各荷重ステップでの部材の変形量や塑性率を逐一追跡することができます。そこで、限界耐力計算法では、部材の変形制限というものをもっと直接的に取り扱うことにしよう、と考えます。たとえば部材の限界塑性率をあらかじめ決めておき、ある荷重ステップでどれかの部材がその限界にたっしたなら、その時点を建物の限界状態とすることができるのではないか、というような考え方です。
となると、つぎは当然、部材の限界塑性率なり限界変形角なりをどのようにして決めるのか、という話になるはずなのだが、これがなかなか。理由はだいたい以下のようなことになる。
 1.部材の限界塑性率をもとめるはっきりした考え方がない。
1.部材の限界塑性率をもとめるはっきりした考え方がない。
 2.部材の変形角というのは、そもそもがデリケートな値なので、解析上のちょっとした仮定によっ
2.部材の変形角というのは、そもそもがデリケートな値なので、解析上のちょっとした仮定によっ
 て敏感に値が動いてしまう。そのような値を指標としたものについての客観的な評価がなかなか難
て敏感に値が動いてしまう。そのような値を指標としたものについての客観的な評価がなかなか難
 しい。
しい。
 3.必ずしも部材の変形角・塑性率だけから建物の限界状態が決まるわけではない。
3.必ずしも部材の変形角・塑性率だけから建物の限界状態が決まるわけではない。
注)「はっきりした考え方がない」といいましたが、じつは国土交通省(建設省)から出されている告示(平12建告第1457号第3)には、部材の限界変形角の計算式が載っていて、「安全限界変位は(途中略)・・・当該階の一の部材が次の式によって計算した部材の限界変形角に達した場合の層間変位以下の変位とする。」と書かれています。この式は部材の曲率から限界変形角を推定するものです(詳細は略します)。しかし実際にはどうなのかというと、(おそらくは上に述べたような理由から)ほとんど誰も使っていない、というのが現状のようです。この告示の内容に即した実例を紹介するというのが本来の役目であるはずの「計算例と解説」ですら、この式は採用していません。この本では、後で述べるような「建物の限界状態における個々の部材の変形能力の検証」が、間接的にこの告示の内容を満足させることにつながるのである、という立場をとっています。
そこでどうするのか。「ガイドライン」や「計算例と解説」の例題では、次の考え方をとっているのだ。
なんらかの工学的判断にもとづいた「層間変形角の限界値」をあらかじめ決めておき、ある荷重ステップにおいてどこかの階の層間変形角がその限界値にたっしたなら、その時点をもって建物の限界状態とする。さらに、その限界状態における個々の部材の変形能力を検証する。
つまり、『建物の限界状態をあらわす層間変形角』を最初に決めておき、その限界状態における個々の部材の変形量が一定の限界の中にあるのであれば、最初に決めた建物の限界状態の正当性が担保されることになる、という考え方を採用している。しかし、これはもちろん、最初に決めた『建物の限界状態をあらわす層間変形角』が正当なものであれば、という話なのだが。となると、問題は、最初の前提である『建物の限界状態をあらわす層間変形角』をどのようにして決めるのか、になるけれども、これまた『はっきりした考え方はない』のです。というような事情なので、『建物の限界状態をあらわす層間変形角をどのようにして決めたらよいのか』ということを筋道だて話すのは、とても難しいのですが、・・・・・・・・・
そこで、『実際にはどのようにやられているのか』ということを紹介することとしよう。
 鉄骨造の場合
鉄骨造の場合
鉄骨造の計算例として目にすることができるのは、「計算例と解説」の「設計例1(鉄骨造11階建事務所)」くらいしかないのですが・・・・・ ここでは、層間変形角の限界値を下のように定めている。
純ラーメン方向 1/50
ブレースを含む方向 1/60
この数値の具体的な根拠についてはとくに書かれてはいないのだが、『建物として許容できる最大限の層間変形角はだいたい 1/50 程度くらいと考えられるますが、ブレースがある方向については、これに若干の安全率を見込んだ』というようなことと考えられる。
『建物として許容できる最大限の層間変形角』という考え方については、『P-⊿効果』の面からの考察が一般的。この『P-⊿効果』とは、次の図にしめすように、『建物が水平方向に大きく変形すると重力加速度(g)の効果によって付加的なせん断力が発生する』という仕組みのことをいいます。
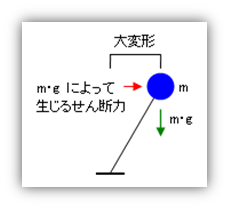
つまり、層間変形角が 1/50 を超えるような大変形のもとでは P-⊿効果が無視できなくなり、解析の結果そのものがあまり当てにならない。だから、層間変形角の限界値は最大でも 1/50 程度にすべきである。 ということになる。つぎは『建物の限界状態における個々の部材の変形能力の検証』ですが、ここでは以下のような方法をとっています。
 1.いくつかの論文を参考にして各部材の「限界塑性率」をもとめ、限界状態における塑性率がこれを上回っていないことを検証する。注)
1.いくつかの論文を参考にして各部材の「限界塑性率」をもとめ、限界状態における塑性率がこれを上回っていないことを検証する。注)
 2.従来の計算方法にある「保有耐力横補剛」「保有耐力接合部」の検証を行なう
2.従来の計算方法にある「保有耐力横補剛」「保有耐力接合部」の検証を行なう
 3.柱梁接合部(パネルゾーン)の耐力と梁の耐力の比にかんする検証を行なう
3.柱梁接合部(パネルゾーン)の耐力と梁の耐力の比にかんする検証を行なう
注) ちなみに、ここでもとめた「限界塑性率」はどの程度の値になるのかというと、だいたい 5 から 6 くらいの値になっています。これは前にいった、「部材ランクを A にしておけば、限界塑性率はだいたい 5 から 6 くらいの値になる」ということと符合しています。それならば、「部材ランクが A で、かつ限界状態の塑性率が 4 以下になっていれば OK 」というやり方だってあるのではないか、という気もしてきます。 ただし、これはなにも、「このとおりにやりなさい」ということではなく、「こういう考え方もありますよ」という程度に考えておくべきものでしょう。「性能規定」という性格からすれば、これは当然のことです。
 鉄筋コンコンリートの場合
鉄筋コンコンリートの場合

「計算例と解説」の「設計例 2(鉄筋コンクリート造 5 階建事務所)」では、層間変形角の限界値を下のようにさだめている。
 純ラーメン方向 1/65
純ラーメン方向 1/65
 耐震壁を含む方向 1/150
耐震壁を含む方向 1/150
これについても明確な根拠は書かれてはいないけど、その背景には、日本建築学会「鉄筋コンクリート造建築物の靭性保証型耐震設計指針・同解説」にある、『(終局限界変形は)特に検討しない場合は、純フレーム構造では 1/80 以上、耐震壁フレーム構造では 1/100 以上とする』という記述(P.82)があるといえます。
また当然、以下にしめすような『建物の限界状態における個々の部材の変形能力の検証』の結果をフィードバックして試行錯誤的に定めた、ということも考えられる。
注)「特に検討しない場合」とあるのですから、当然、「特に検討する場合」の方法もあることになりますが、それについては、この本、あるいは日本建築学会「鉄筋コンクリート造建築物の終局強度型耐震設計指針・同解説」などを参照してください。また、「ガイドライン」には、従来の計算方法にある「構造特性係数(Ds)」の値から限界変形角をもとめる、という簡便な方法も紹介されています(P.151)。
いずれにしても、「これ」といった方法はない、ということです。
『建物の限界状態における個々の部材の変形能力の検証』は以下のように行なう。
1.日本建築学会「鉄筋コンクリート造建築物の靭性保証型耐震設計指針・同解説」にもとづいて付着強度とせん断強度の検討をする。
2.日本建築学会「鉄筋コンクリート造建築物の終局強度型耐震設計指針・同解説」にもとづいて柱の軸力制御の検討をする。
もちろん先に述べたとおり、これも『このとおりにやりなさい』ではなく、『こういう考え方もあります』というような性格のものと思ってほしいのです。
『ガイドライン』のほうにも『適用例』として三ケースについての計算例が載っているのだが、ここでは、層間変形角の限界値を基本的に 1/50 としている。これは、先に述べたような『P-⊿効果を勘案した限界値』というようなものかと推測できる。ただし、『変形量をおさえることを意図した設計(適用例 2)』では、これを 1/75 としている。また、変形能力の検証の方法は、上に述べた『計算例と解説』と同じですが、つねに最新の研究や論文に目配りできるような環境にいるわけではありません(ごく少数の例外を除いて)。結局私たちとしては、「こういうやり方もある・ああいうやり方もある」というストックをたくわえておき、必要に応じてそれを出し入れできるような、そういう能力を養っておけばいい、ということなんじゃないでしょうか?
さて、ここまで変位の限界について説明してきました。これらは建物の『安全性』の検証にかかわる話です。『建物の安全性の検証』」とは何か。結局、『建物が崩壊しないことをたしかめる』こととなる。何にたいして建物が崩壊しないことをたしかめるのかとは、『きわめてまれに起きる(500年に一度くらいの)地震』にたいしてです。もちろん、今の話は順序が逆なのかもしれない。きわめてまれに起きる地震、つまり建物の耐用期間内に遭遇する可能性がある最大級の地震にたいして建物はどのようにあるべきか、という問いがまずあって、それにたいする答えが『建物が崩壊しないことを最低限の条件とすればよい』である。というのが話の正しい順序。(いうまでもなく、これは「法令にさだめる最低限の性能」ですから、「きわめてまれに起きる地震にたいして建物を弾性範囲内にとどめる」、あるいは「ひび割れの一つも入れさせない」という設計だってありえます。) ここで、これまでの復習をかねながら、建物の安全性、つまり安全限界にかんする検証の方法をふりかえってみると、
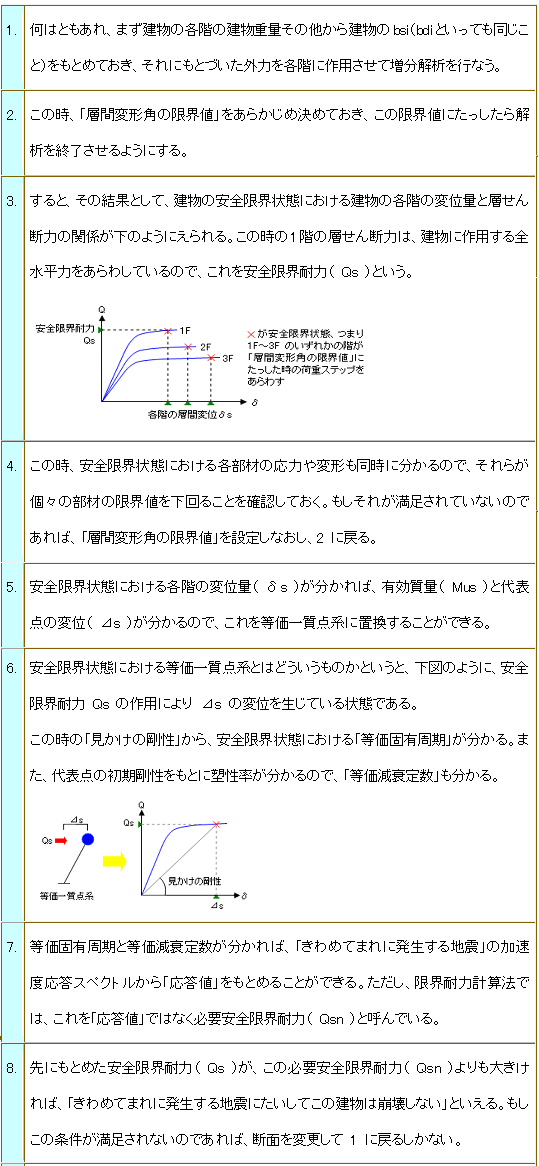
ここで注目しておきたいのは、『安全限界耐力』にしても『必要安全限界耐力』にしても、これらは等価一質点系のせん断力、言い換えれば建物に作用する水平力の総和、ようするに『一階の層せん断力』を指している、ということだ。 結局、『建物が安全であるかどうかは、一階の層せん断力だけを見れば分かる』ということになるのですが。
なぜそうなのか、については今さら説明を要しないかもしれないけど、一応下に図示しておくと、
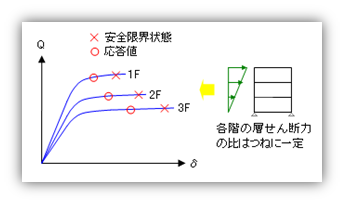
上図は増分解析法における各階の Q-δ なのだが、ここで、各階の応答値が安全限界状態にたっしていないのであれば、その応答値は、各階ともかならず安全限界状態の内側(原点に近い側、つまり層せん断力や層間変位が小さい側)にあるはず。いうまでもなく、決められた外力分布にもとづいて荷重を漸増させているので、各階の層せん断力はつねに一定の比を保ったまま増加するから。結局、上図のように建物の各階の Q-δ 上にいちいち応答値をプロットする必要はなくて、一階の層せん断力、つまり等価一質点系の限界値と応答値だけ見ておけばことが済む、ということになる。下にあるのが等価一質点系の Q-δ だが、ここにある安全限界耐力よりも応答値が小さければそれで良い、ということとなる。
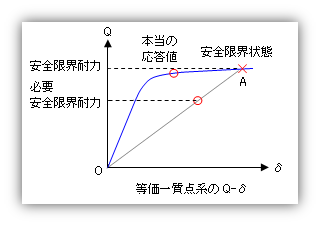
ところで、上の図はちょっとヘンだよね。Q-δ の曲線上に応答値をしめす丸印を書き入れているけど、これとは別に、原点と限界状態をあらわす点 A をむすんだ直線 OA にも丸印を書き入れ、この点を「必要安全限界耐力」としている。これはどういうことなのだろう?
応答値のもとめ方で、「塑性化後の応答も弾性の場合とおおむね同じ考え方でもとめることができる」と説明した。 これは何をどうしたのかというと、塑性化後の建物がつねに上図の直線 OA 上を行き来して振動する、と仮定しました。 だから当然、応答値もこの直線上にえられることとなる。これが『必要安全限界耐力』なのです。
しかし、実際の建物の振動履歴は曲線 OA 上になければいけないはず。だから、直線 OA 上にえられた応答値は『本当の応答値』ではなく、『本当の応答値』は曲線 OA 上にあるはずだ、ということになるのだが。なんだ、今までさんざん『応答値のもとめ方』を話しておいて、『じつはあれはニセモノでした』はないじゃないか、と詰め寄られると困るけど、しかし、まったくのニセモノというわけではないのだよ。上の図を見ると分かるとおり、直線上にえられる必要安全限界耐力が安全限界耐力よりも小さければ、『本当の応答値』もかならず安全限界耐力よりも小さくなる。つまり、必要安全限界耐力が安全限界耐力よりも小さいことを証明しさえすれば、べつに『本当の応答値』をもとめなくて建物の安全性が保障される、ということです。
というようなわけで、限界耐力計算では、『本当の応答値』をもとめなくても、『必要安全限界耐』をもとめてそれが限界耐力を下回っていることを証明すれば、それでいいということになっているのだ。それから、上の図を見ながらついでにもう一つおぼえておきたいのは、必要安全限界耐力と安全限界耐力が一致している場合にかぎり、必要安全限界耐力は『本当の応答値』になるということ。
注) 限界耐力計算法がこのような立場をとっている背景には、「必要安全限界耐力なら簡単にもとまるが、本当の応答値をもとめるのはかなりヤヤコシイ」という事情があり不必要に複雑な解析はしない。


